Quantifier son impact en évaluation : le rôle des statistiques inférentielles
Si, de manière générale, les statistiques sont bien connues du grand public, les statistiques inférentielles le sont moins. Leur rôle principal, en évaluation d’impact social, consiste à « faire parler » des données récoltées via des questionnaires de manière rigoureuse et approfondie. Alors, pourquoi est-ce intéressant d’intégrer les statistiques inférentielles dans son évaluation d’impact social ? Et comment les utiliser ?
1. Les statistiques inférentielles, un moyen de mieux comprendre ses impacts
Les statistiques inférentielles sont réalisées en complément des statistiques descriptives[1]. Leur rôle est de prouver l’existence de liens entre des variables[2], par exemple entre des données d’impact et d’autres types de données (comme des données de performance ou de caractérisation). En effet, certaines variables peuvent être liées les unes aux autres : par exemple la taille et l’âge d’un enfant.
Pour une organisation, mieux comprendre les liens entre les variables revient à mieux comprendre ses impacts et donc prendre des décisions stratégiques éclairées.
Les statistiques inférentielles se réalisent en 3 étapes clés :
1ère étape : formuler des hypothèses : Une organisation émet une ou plusieurs hypothèses de départ qui statuent sur l’existence ou non d’un lien entre deux variables. Autrement dit, elle se demande si deux variables sont (in)dépendantes l’une de l’autre.
2ème étape : réaliser des statistiques inférentielles : L’organisation mesure les variables faisant l’objet de l’hypothèse. L’organisation peut résumer et présenter les données recueillies sous forme de tableaux ou de graphiques, il s’agit alors de statistiques descriptives. Mais pour tester l’hypothèse de départ, l’organisation doit mobiliser des statistiques inférentielles. Elles se basent sur la réalisation de tests statistiques consistant à croiser des données entre elles (régression linéaire, Chi2, test de Student…). Ces derniers sont choisis selon des critères[3] et peuvent être effectués via des logiciels de traitement statistiques comme SPSS ou encore R Studio.
3ème étape : interpréter les résultats et conclure : En fonction des résultats obtenus grâce aux tests, il est possible de valider ou de rejeter les hypothèses de départ. Cela prouve l’existence ou non d’un lien entre deux variables.
2/ Exemple pratique d’utilisation des statistiques inférentielles
Afin d’éclaircir le rôle des statistiques inférentielles et la manière dont celles-ci peuvent aider à la prise de décision, nous proposons un exemple.
Contexte. Une université déploie un programme de cours avec des formats différents : l’un en présentiel (sur place) et l’autre à distance (en visioconférence). Elle souhaite statuer sur un format de cours identique pour tous : présentiel uniquement, à distance uniquement ou hybride.
Formulation de l’hypothèse. Elle se questionne notamment sur les effets du programme à distance concernant la prise de parole des étudiants. En effet, les enseignants craignent que les cours à distance pénalisent les étudiants dans le développement de leurs compétences en prise de parole.
L’université émet l’hypothèse que les étudiants suivant le programme en présentiel ont davantage développé leurs compétences en prise de parole que les étudiants suivant le programme à distance ; c’est-à-dire qu’il existe un lien entre la variable « développer ses compétences en prise de parole » et la variable « format de cours ».
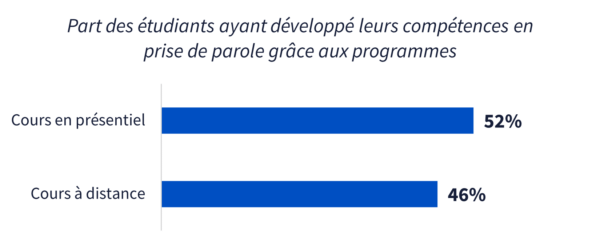
Réalisation d’un test statistique. L’université mesure le développement de compétences en prise de parole pour chaque groupe d’étudiants ayant suivi les cours avec des formats différents. La figure ci-dessous décrit graphiquement les résultats (statistiques descriptives) pour chaque groupe, mais une comparaison « à l’œil nu » ne permet pas d’observer une différence incontestable entre les groupes et donc d’établir un lien entre les deux variables.
Afin de prouver si cette différence apparaissant « à l’œil nu » est réelle, l’université mobilise un test statistique.
Interprétation du test. Le test rejette l’hypothèse de départ ; il n’existe pas de lien entre les deux variables. Autrement dit, dans cette situation, le format de cours n’influence pas l’amélioration des étudiants dans l’exercice de la prise de parole.
Grâce aux statistiques inférentielles l’université peut statuer sur un format unique et décide d’opter pour un programme hybride.
En conclusion…
En évaluation d’impact, les statistiques inférentielles sont une manière de mieux comprendre et objectiver ses impacts sociaux. Elles permettent de confirmer ou de rejeter l’existence d’un lien entre deux variables que l’on croit voir à l’œil nu, peu importe le type de comparaison (programme A vs programme B comme dans l’exemple ci-dessus, mais aussi public A vs public B, mesure en amont du programme vs en aval etc.). C’est pourquoi, les statistiques inférentielles révèlent parfois des résultats différents de ceux des statistiques descriptives. Plus une organisation souhaitera avoir un degré fin d’analyse et de rigueur, plus elle aura tendance à recourir aux statistiques inférentielles.
Grâce à ces éléments, les organisations peuvent tirer des enseignements, prendre des décisions pour améliorer leurs programmes ou innover.
Pour citer cet article : Improve, Quantifier son impact en évaluation : le rôle des statistiques inférentielles, janvier 2024
[1] Les statistiques descriptives permettent de résumer les données de manière simple. Il est possible de les définir comme « ce qui est visible à l’œil nu ». À la différence des statistiques inférentielles, elles ne permettent pas de déterminer l’existence de liens entre des variables.
[2] En statistique, une variable est une caractéristique étudiée sur l’ensemble d’une population, mais dont la valeur peut varier selon les individus.
[3] Comme la taille de l’échantillon d’une population ou encore le type de variable étudiée.

